On A Plane ...
Line
General Form: \( A x + B y + C = 0 \) Form 1: \( y = k x + b \)
Theorem 1
\( A x + B y + C \) have the same sign \( \iff \) Points are on the same side
\( A x + B y + C \) have the different sign \( \iff \) Points are on the different side
NCEE
Theorem 2
If the range of angles is continuous
90 degree is in the range and it is not the endpoint \( \iff \) the range of slope is discontinuous
90 degree is in the range \( \iff \) there is \( \infty \) in the expression of the range of slope
NCEE
NCEE: Parallel; Vertical and Auxiliary Rounding
Parametric Equation
Procedure: reflect a point across a line
Given
Line \( Ax+By+C=0 \)
Point 0 \( P_0(x_0,y_0) \)
,
\(d_2=\frac{Ax_0+By_0+C}{A^2+B^2}\)
Point 1 \(x=x_0-2d_2A\) \(y=y_0-2d_2B\)
Circle
\((x-a)^2+(y-b)^2=r^2\)
Tangent:\((x-a)(x_0-a)+(y-b)(y_0-b)=r^2\)
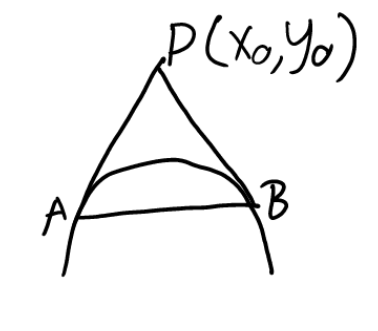
Line AB: \((x-a)(x_0-a)+(y-b)(y_0-b)=r^2\)
NCEE
NCEE: Relations between multiple circles
Ellipse
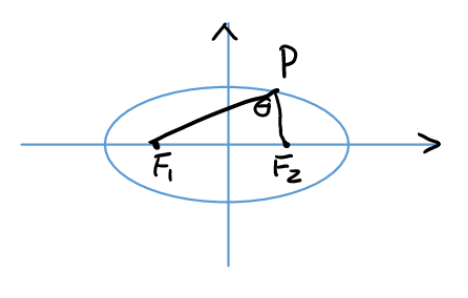
Theorem:
\( S_{\Delta F_1 P F_2} = \frac{1}{2} \left\lvert F_1F_2 \right\rvert \left\lvert y_p \right\rvert = c \left\lvert y_p \right\rvert \)
\( S_{\Delta F_1 P F_2} = b^2 tan \frac{\theta}{2} \)
Theorem 1
\(c\in[sin\frac{\theta}2,1)\)
NCEE
Theorem 2
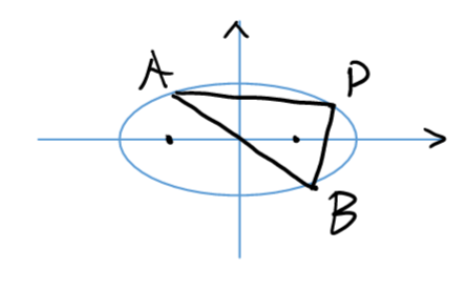
Ellipse/Hyperbola \(k_{PA}\cdot k_{PB}=e^2-1\)
Proof: \(x^2+(\frac{a}{b}y)^2=a^2\) Then regard it as a circle
(or, can alternatively be deduced from point difference method)
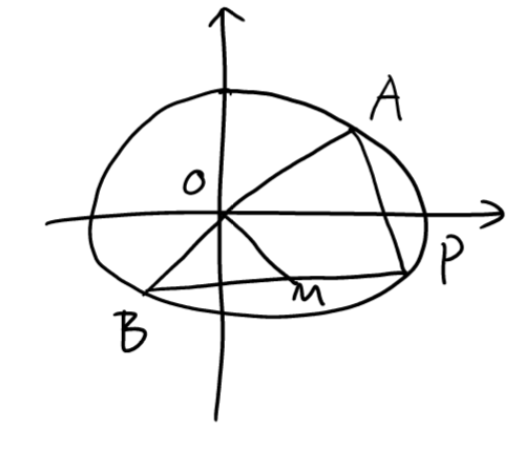
Ellipse/Hyperbola \(k_{MO}\cdot k_{BP}=e^2-1\)
Hyperbola
\( S_{\Delta F_1 P F_2} = b^2 cot \frac{\theta}{2} \)
NCEE
Parabola
Theorem 1
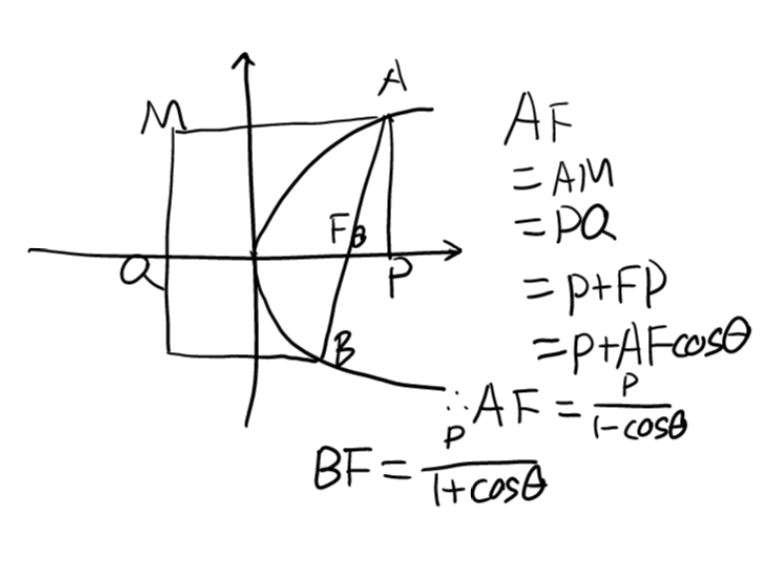\(AB=AF+BF=\frac{2p}{1-cos^2\theta}=\frac{2p}{sin^2\theta}\)
Ellipse/Hyperbola: \(AF=\frac{\frac{b^2}a}{1-e\cdot cos\theta}BF=\frac{\frac{b^2}a}{1+e\cdot cos\theta}\)
Parabola/Ellipse/Hyperbola: \(AF=\lambda BF\iff \left\lvert e\cdot cos\theta\right\rvert=\left\lvert\frac{\lambda-1}{\lambda+1}\right\rvert\)
Mnemonic
\(\frac{p}{1\pm\left\lvert cos\theta\right\rvert}\) Long minus;short add
NCEE
设点联立韦达
1
Ellipse:
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) and \(Ax+By+C=0\)
\(\iff\)
\(\Delta=4b^2B^2a^2(a^2A^2+b^2B^2-C^2)\)
\(\Delta'=a^2A^2+b^2B^2-C^2\)
Hyperbola: \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\iff\frac{x^2}{a^2}+\frac{y^2}{(b i)^2}=1\) so \(\Delta'=C^2+b^2B^2-a^2A^2\)
NCEE
2
\(\alpha x^2+\beta y^2=\gamma\) and \(Ax^2+By+C=0\) \(\iff\) \((\alpha B^2+\beta A^2)x^2+2CA\beta x+\beta C^2-\gamma B^2\)
Ellipse: \(l=\frac{2\sqrt{a^2b^2(A^2+B^2)\Delta'}}{a^2A^2+b^2B^2}\)
Hyperbola: \(l=\frac{2\sqrt{a^2b^2(A^2+B^2)\Delta'}}{\left\lvert a^2A^2+b^2(Bi)^2 \right\rvert}=\frac{2\sqrt{a^2b^2(A^2+B^2)\Delta'}}{\left\lvert a^2A^2-b^2B^2 \right\rvert}\)